383. Histogram

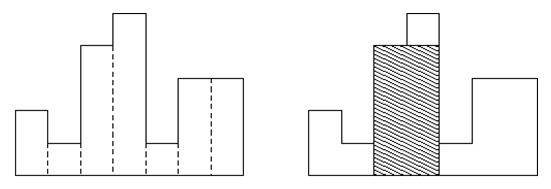
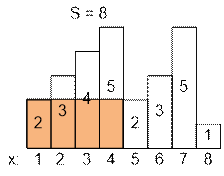
The histogram is a polygon formed from the sequence of rectangles, aligned on a common baseline. The rectangles are of equal width but may have different heights. For example, the figure on the left shows the histogram, which consists of rectangles with heights of 2, 1, 4, 5, 1, 3, 3. All rectangles in this figure have a width equal to 1.

Usually, histograms are used to represent discrete distributions, for example, the frequency of characters in the texts. Note that the order of the rectangles is very important. Calculate the area of the largest rectangle in the histogram, which is also located on a common baseline. The figure on the right is the shaded figure is equal to the largest aligned rectangle on the image histogram.

Input. First line contains the number n (0 ≤ n ≤ 10⁶) of rectangles of the histogram. This is followed by n integers h₁, ..., h_n (0 ≤ h_i ≤ 10⁹). These numbers indicate the height of the rectangle of the histogram from left to right. The width of each rectangle is equal to 1.

Output. Print the area of the largest rectangle in the histogram. Remember that this rectangle should be on a common baseline.

Sample input	Sample output
7 2 1 4 5 1 3 3	8

SOLUTION

data structures - stack

Algorithm analysis

O(n²) implementation. For each i-th rectangle of width 1, try to push its borders: left to the left and right to the right as long as possible (that is, the heights of all rectangles from left to right are at least h_i, 1 ≤ left ≤ i ≤ right ≤ n). We get the largest possible rectangle inscribed in the histogram, which rests against the top of the i-th rectangle. We are looking for the maximum among all such rectangles. This solution gives Time Limit.

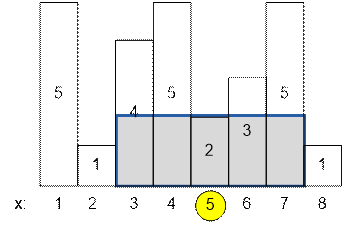
Let’s inscribe the maximum rectangle abutting the top of the 5-th rectangle. Its borders will be [left; right] = [3; 7], the height is 2. The area is (right – left + 1) * h₅ = (7 – 3 + 1) * 2 = 5 * 2 = 10.

O(n) implementation. Each rectangle is characterized by abscissa i and height h_i. Let’s create a stack of pairs (i, h_i) – characteristics of rectangles. Let’s introduce into consideration two additional rectangles with heights h₀ = -1, h_n+1 = 0. We push the zero rectangle with height -1 to the stack (push the pair (0, -1) to the stack). These heights are chosen in order to:

· the zero’s rectangle has never been popped from the stack;

· processing the last rectangle with a height of 0 will pop all rectangles except the zero from the stack;

Let the current be the i-th rectangle with abscissa i and height h_i. Then:

· If its height is greater than the height of the rectangle at the top of the stack, then push the i-th rectangle to the stack.

· While the height of the current rectangle (i, h_i) is less than or equal to the height of the rectangle at the top of the stack (x, h_x) (that is h_i ≤ h_x), then we pop the rectangle from the stack and compute the area of the maximum rectangle inscribed in the histogram. Suspicious for the maximum will be a rectangle with sides i – x (it starts at the abscissa x and ends at the abscissa i – 1) and h_x. Let the last rectangle of width 1 pushed out of the stack has characteristics (j, h_j) (h_j ≥ h_i). Then the pair (j, h_i) should be pushed to the stack.

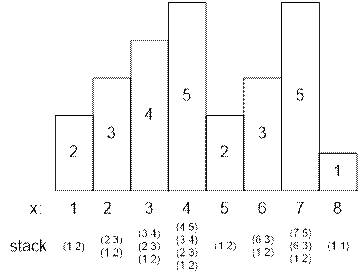
Example

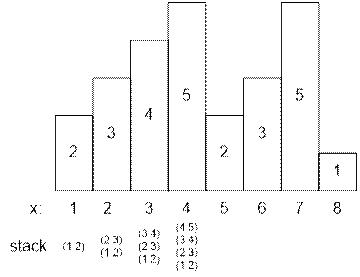
Let we have reached the fourth rectangle inclusive. Since the heights of the rectangles went up to it, they were added to the stack. The next fifth rectangle has a height of 2. Sequentially we extract the rectangles from the stack, the heights of which are strictly greater than the current one and recalculate the areas of the resulting maximum rectangles:

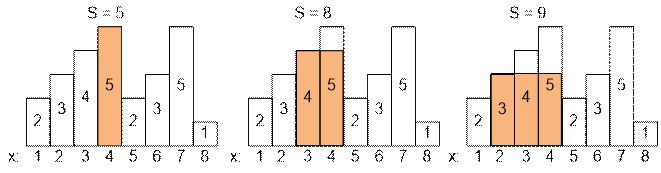
The fifth rectangle has a height of 2, we extract the first rectangle from the stack, recalculate the area:

Only a zero rectangle with a height of -1 remains on the stack. The last rectangle popped from the stack has characteristics (j, h_j) = (1, 2). The current one under consideration is rectangle number 5 with height 2, that is (i, h_i) = (5, 2). Therefore, we push on the stack a rectangle with parameters (j, h_i) = (1, 2). In the future, the state of the stack will be as follows:

Algorithm realization

In the Node structure, store the x abscissa and the Height of the rectangle in this abscissa. Declare a stack s from these structures.

struct Node

{

int x;

int Height;

Node(int x, int Height) : x(x), Height(Height) {};

};

stack<Node> s;

Read the input data. Consider the heights of the zero and (n + 1)-th rectangles to be equal to -1 and 0, respectively. Push the zero rectangle to the stack. Since its height is -1, it will never be popped off the stack.

scanf("%d",&n);

s.push(Node(0,-1));

Process the rectangles sequentially. The area of the maximum rectangle covering the histogram is computed in the res variable.

res = 0;

for(i = 1; i <= n + 1; i++)

{

Read the height of the i-th rectangle. Its abscissa x equals to i. If i = n + 1, then its height is zero: at the end it is necessary to pop all rectangles from the stack except the first one with a height of -1 and recompute the required area.

if (i <= n) scanf("%d",&h); else h = 0;

int x = i;

while (h <= s.top().Height)

{

x = s.top().x; hPrev = s.top().Height; s.pop();

area = 1LL * hPrev * (i - x);

if (area > res) res = area;

}

s.push(Node(x,h));

}

Print the area of the largest rectangle.

printf("%lld\n",res);

Realization for O(n²)

#include <stdio.h>

#define MAX 1000010

long long h[MAX];

int i, n, left, right;

long long area, res;

int main(void)

{

scanf("%d",&n);

for(i = 1; i <= n; i++)

scanf("%d",&h[i]);

res = 0;

for(i = 1; i <= n; i++)

{

left = right = i;

while(left > 1 && h[left-1] >= h[i]) left--;

while(right < n && h[right+1] >= h[i]) right++;

area = (right - left + 1) * h[i];

if (area > res) res = area;

}

printf("%lld\n",res);

return 0;

}